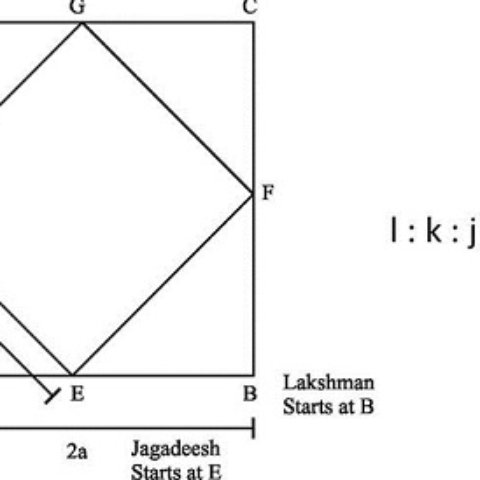
Consider a square ABCD. EFGH is another square obtained by joining the midpoints of the sides of the square ABCD where E, F , G amd H are the midpoints of AB, BC, CD and DA respectively. Lakshman and Kanika start from points B and D respectively at speeds ‘l’ kmph and ‘k’ kmph respectively and travel towards each other along the sides of the square ABCD. Jagadeesh starts from Point E and travels along the Square EFGH in the anti-clockwise direction at ‘j’ kmph. Lakshman and Kanika meet for the second time at H where Jagadeesh also meets them for the first time. If l : k : j is 1: 3 : 5√2 then the distance travelled by Jagadeesh is

Lakshman and Kanika convene for the second time at point H, where Jagadeesh also encounters them for the first time, covering a distance of √2 units.

Lakshman and Kanika initiate their journeys from points B and D respectively, at speeds ‘l’ kmph and ‘k’ kmph. They proceed towards each other along the sides of the square ABCD, finding themselves at a distance of 4a from one another. As they are diametrically positioned, their relative distance would remain 4a regardless of their chosen directions. Thus, to rendezvous for the first time, they must collectively cover a distance of 4a.

For their second encounter, they would have traversed an additional 8a jointly, essentially encompassing the entire perimeter of the square.

Consequently, by their second meeting, they would have journeyed a combined distance of 12a. Given that their speeds are in a 1:3 ratio, Lakshman would have covered 3a while Kanika would have traveled 9a. In this scenario, Lakshman moves in the direction of BADC, while Kanika moves in the direction of DABC. Their initial encounter transpires at point E and their subsequent meeting occurs at point H.

Meanwhile, Jagadeesh traverses the square EFGH in an anti-clockwise trajectory at ‘j’ kmph, making his first encounter with Lakshman and Kanika. Although it remains unknown how many laps Jagadeesh completes before this encounter, the ratio of Lakshman’s speed to Jagadeesh’s is 1:5√2. Thus, their respective distances covered align with this ratio. Therefore, if Lakshman has traveled a distance of 3a, Jagadeesh would have covered a distance of 3a × 5√2 to arrive at H.

Hence, Jagadeesh travels 7.5 × √2 times the side length of the square ABCD to reach H, as indicated by answer choice (a).